 Am Anfang schuf Gott
Adam und Eva. Und in Adam war es
wüst und leer, und es wollte einfach nicht Licht werden in seinem
Gehirn, wo
Finsternis und Chaos herrschten. Und Gott sprach: „Es werde Ordnung in
der
Wirre der Gedanken und Begriffe und der Name dieser Ordnung sei
Mathematik.“
Und Gott sah, dass die Mathematik gut war. Da schied Gott die Zahlen
von den
Rechenzeichen und nannte die natürlichen
Zahlen ℕ und die
Rechenzeichen Plus und Minus. So ward aus Summe und Differenz der erste
Tag.
Am Anfang schuf Gott
Adam und Eva. Und in Adam war es
wüst und leer, und es wollte einfach nicht Licht werden in seinem
Gehirn, wo
Finsternis und Chaos herrschten. Und Gott sprach: „Es werde Ordnung in
der
Wirre der Gedanken und Begriffe und der Name dieser Ordnung sei
Mathematik.“
Und Gott sah, dass die Mathematik gut war. Da schied Gott die Zahlen
von den
Rechenzeichen und nannte die natürlichen
Zahlen ℕ und die
Rechenzeichen Plus und Minus. So ward aus Summe und Differenz der erste
Tag.
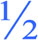 Und
Gott sprach: „Es werde ein Bruchstrich zwischen den Zahlen, der da
scheide
zwischen Oben und Unten.“ Da machte Gott den Bruchstrich und schied die
obere
Zahl von der unteren Zahl. Und es geschah so. Und Gott nannte das Oben
den Zähler
und das Unten den Nenner. Da ward aus Bruchteil und Ganzem der zweite
Tag.
Und
Gott sprach: „Es werde ein Bruchstrich zwischen den Zahlen, der da
scheide
zwischen Oben und Unten.“ Da machte Gott den Bruchstrich und schied die
obere
Zahl von der unteren Zahl. Und es geschah so. Und Gott nannte das Oben
den Zähler
und das Unten den Nenner. Da ward aus Bruchteil und Ganzem der zweite
Tag.
 Dann
machte Gott das Gleichheitszeichen, das Kleiner und das Größer, formte
negative
und positive Zahlen zu Termen und verteilte sie auf der linken und der
rechten
Seite des Zeichens. Und Gott hob das X und das Y aus dem Alphabet
heraus und
machte sie zu Variablen. Da erschuf Gott die Aussagen und nannte sie
Wahr und
Falsch. So ward aus Gleichung und Ungleichung der dritte Tag.
Dann
machte Gott das Gleichheitszeichen, das Kleiner und das Größer, formte
negative
und positive Zahlen zu Termen und verteilte sie auf der linken und der
rechten
Seite des Zeichens. Und Gott hob das X und das Y aus dem Alphabet
heraus und
machte sie zu Variablen. Da erschuf Gott die Aussagen und nannte sie
Wahr und
Falsch. So ward aus Gleichung und Ungleichung der dritte Tag.
 Und
Gott sprach: „Es sollen sich sammeln alle Zahlen, die positiven und
negativen,
die abbrechenden und die periodischen, die Potenzen und die Wurzeln in
einer
einzigen Menge.“ Und so geschah es. Und Gott nannte die Menge die
Reellen
Zahlen und sprach zu Adam: „Rechne mit ihnen nach den Gesetzen der
Algebra und
du wirst den binomischen Lehrsatz beweisen.“ So ward aus Basis und
Exponent der
vierte Tag.
Und
Gott sprach: „Es sollen sich sammeln alle Zahlen, die positiven und
negativen,
die abbrechenden und die periodischen, die Potenzen und die Wurzeln in
einer
einzigen Menge.“ Und so geschah es. Und Gott nannte die Menge die
Reellen
Zahlen und sprach zu Adam: „Rechne mit ihnen nach den Gesetzen der
Algebra und
du wirst den binomischen Lehrsatz beweisen.“ So ward aus Basis und
Exponent der
vierte Tag.
 Und
Gott schuf gerade und krumme Linien, Strecken und Kreise, ebene und
gewölbte
Flächen und Körper der verschiedensten geometrischen Formen mit ihren
Winkeln,
Längen, Oberflächen und Volumina. Und Gott erschuf den Zirkel, das
Lineal und
das Dreieck, gab sie Adam, auf dass er alles zeichne und berechne und
sich daran
erfreue. Und Gott sah, dass es gut war. So ward aus Parallel und
Orthogonal der
fünfte Tag.
Und
Gott schuf gerade und krumme Linien, Strecken und Kreise, ebene und
gewölbte
Flächen und Körper der verschiedensten geometrischen Formen mit ihren
Winkeln,
Längen, Oberflächen und Volumina. Und Gott erschuf den Zirkel, das
Lineal und
das Dreieck, gab sie Adam, auf dass er alles zeichne und berechne und
sich daran
erfreue. Und Gott sah, dass es gut war. So ward aus Parallel und
Orthogonal der
fünfte Tag.
 Und
Gott sprach: „Es werde das Koordinatensystem mit seinem Ursprung,
seinen
Quadranten, mit Ordinate und Abszisse und ihrem Maßstab. In dieses
sollen sich
einfügen Geraden, Parabeln, Hyperbeln und Kurven höherer Ordnung mit
ihren Nullstellen,
Hoch- und Tiefpunkten und ihren Asymptoten.“ Und Gott nannte die
Hochpunkte
Maxima und die Tiefpunkte Minima, jeden nach seiner Art. Viele davon
sollten
folgen aufeinander und so formte er den Einheitskreis und die
trigonometrischen
Funktionen. Zuletzt erschuf Gott den Logarithmus und machte auch daraus
eine
Funktion. Und Gott betrachtete sein Werk mit Wohlgefallen. Da ward aus
Sinus
und Kosinus der sechste Tag.
Und
Gott sprach: „Es werde das Koordinatensystem mit seinem Ursprung,
seinen
Quadranten, mit Ordinate und Abszisse und ihrem Maßstab. In dieses
sollen sich
einfügen Geraden, Parabeln, Hyperbeln und Kurven höherer Ordnung mit
ihren Nullstellen,
Hoch- und Tiefpunkten und ihren Asymptoten.“ Und Gott nannte die
Hochpunkte
Maxima und die Tiefpunkte Minima, jeden nach seiner Art. Viele davon
sollten
folgen aufeinander und so formte er den Einheitskreis und die
trigonometrischen
Funktionen. Zuletzt erschuf Gott den Logarithmus und machte auch daraus
eine
Funktion. Und Gott betrachtete sein Werk mit Wohlgefallen. Da ward aus
Sinus
und Kosinus der sechste Tag.
 Am
siebten Tage aber ruhte Gott. Und er gab Adam die Logarithmentafel und
sprach: „Siehe,
ich gebe in deine Hände das ganze mathematische Paradies. Nun darfst du
addieren, subtrahieren und multiplizieren, du darfst radizieren und
potenzieren. Nur durch die
Zahl 0 darfst
du niemals dividieren, denn diese Zahl ist ein Geschöpf des Fürsten der
Finsternis.“ Aber
die Schlange war listiger als alle Tiere auf dem Felde und sie sprach
zu Eva: „An
dem Tage, da ihr durch 0 dividiert, werden eure Augen aufgetan und ihr
werdet lernen,
was richtig und was falsch ist!“ Und das törichte Weib nahm Adam
beiseite und
sprach zu ihm: „Dividiere und die Gleichung wird viel einfacher werden
als
vorher. Und
Adam fasste sich ein Herz und dividierte durch 0. Da wurden ihnen
beiden die Augen
aufgetan, und sie wurden gewahr, dass sie dumm waren. Und Adam
versteckte sich
mit seinem Weibe vor dem Angesicht Gottes des Herrn unter den Bäumen im
Garten.
Am
siebten Tage aber ruhte Gott. Und er gab Adam die Logarithmentafel und
sprach: „Siehe,
ich gebe in deine Hände das ganze mathematische Paradies. Nun darfst du
addieren, subtrahieren und multiplizieren, du darfst radizieren und
potenzieren. Nur durch die
Zahl 0 darfst
du niemals dividieren, denn diese Zahl ist ein Geschöpf des Fürsten der
Finsternis.“ Aber
die Schlange war listiger als alle Tiere auf dem Felde und sie sprach
zu Eva: „An
dem Tage, da ihr durch 0 dividiert, werden eure Augen aufgetan und ihr
werdet lernen,
was richtig und was falsch ist!“ Und das törichte Weib nahm Adam
beiseite und
sprach zu ihm: „Dividiere und die Gleichung wird viel einfacher werden
als
vorher. Und
Adam fasste sich ein Herz und dividierte durch 0. Da wurden ihnen
beiden die Augen
aufgetan, und sie wurden gewahr, dass sie dumm waren. Und Adam
versteckte sich
mit seinem Weibe vor dem Angesicht Gottes des Herrn unter den Bäumen im
Garten.
 Da
trieb Gott Adam und Eva aus dem mathematischen Paradies und sprach zu
ihnen: „Weil
ihr durch 0 dividiert habt, sei eure Arbeit verflucht. Im Schweiße
eures
Angesichts sollt ihr euer Leben lang addieren, subtrahieren,
multiplizieren, dividieren,
radizieren, potenzieren, logarithmieren und später differenzieren und
integrieren.
Da
trieb Gott Adam und Eva aus dem mathematischen Paradies und sprach zu
ihnen: „Weil
ihr durch 0 dividiert habt, sei eure Arbeit verflucht. Im Schweiße
eures
Angesichts sollt ihr euer Leben lang addieren, subtrahieren,
multiplizieren, dividieren,
radizieren, potenzieren, logarithmieren und später differenzieren und
integrieren.
 Nie
sollt ihr jemals die Quadratwurzel von 2 durch einen Bruch ersetzen,
nie eine
Zahl für das Symbol ∞ angeben können
oder für
π und e genaue
Werte
finden. Ihr werdet für den Sinus
von vielen verschiedenen Zahlen stets den gleichen Wert erhalten, nie
werden eure
Graphen die Asymptoten kreuzen, obwohl sie ihnen doch beliebig nahe
kommen,
und niemals
werdet ihr einen exakten mathematischen Text hervorbringen.“
Nie
sollt ihr jemals die Quadratwurzel von 2 durch einen Bruch ersetzen,
nie eine
Zahl für das Symbol ∞ angeben können
oder für
π und e genaue
Werte
finden. Ihr werdet für den Sinus
von vielen verschiedenen Zahlen stets den gleichen Wert erhalten, nie
werden eure
Graphen die Asymptoten kreuzen, obwohl sie ihnen doch beliebig nahe
kommen,
und niemals
werdet ihr einen exakten mathematischen Text hervorbringen.“
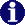 Diese Seite gehört zu www.gsg81.de
Diese Seite gehört zu www.gsg81.de